സമചതുരത്തിന്റെ പരപ്പളവ്
പ്രശ്നങ്ങള്
മുമ്പ് നാം രണ്ട് അളവുകളുമായി ബന്ധപ്പെട്ട പ്രായോഗിക
പ്രശ്നങ്ങള് ചര്ച്ച ചെയ്തപ്പോള് ചില സമവാക്യങ്ങള് രൂപപ്പെടുകയും
അവയുടെ പരിഹാരങ്ങള് കണ്ടുപിടിക്കുകയും ചെയ്തിട്ടുണ്ടല്ലോ. ഇനി മുന് പേജിലെ വീഡിയോയില് നാം കണ്ട സമവാക്യങ്ങളുടെ പരിഹാരം കണ്ടെത്തുന്നതിനുള്ള മാര്ഗങ്ങള് അന്വേഷിക്കാം.
താഴെയുള്ള സമചതുരങ്ങള് പരിഗണിക്കാം. ഇവയുടെ ഓരോന്നിന്റെയും പരപ്പളവ് ചിത്രത്തില് ചേര്ത്തിട്ടുണ്ട്. ഓരോന്നിന്റേയും വശങ്ങളുടെ നീളം എത്രയെല്ലാമായിരിക്കും ?
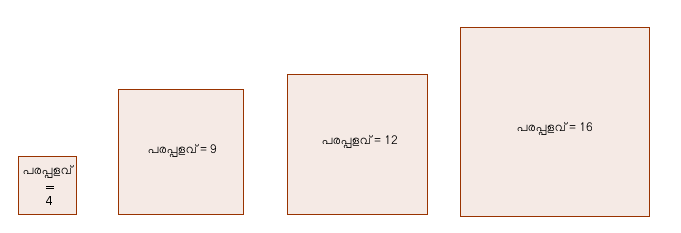
നീളം x എന്നെടുത്താല്,
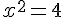
x = 2
ഇതുപോലെ മറ്റു സമചതുരങ്ങളുടേയും വശങ്ങളുടെ വിലകള് കണ്ടുപിടിക്കാന് കഴിയുമല്ലോ.
| എല്ലാ ചിത്രങ്ങളിലും x ന്റെ വില ഒരു പൂര്ണസംഖ്യയായി കണ്ടുപിടിക്കാന് കഴിയില്ല കേട്ടോ. പ്രായോഗികമായി ഒട്ടെല്ലാ സന്ദര്ഭങ്ങളും പൂര്ണ സംഖ്യാ പരിഹാരങ്ങളില്ലാത്തവയാണ് എന്നു കൂടി ഓര്ക്കുക ! |
ചോദ്യം:
ഒരു സമാന്തര ശ്രേണിയുടെ ഒന്നാം പദത്തിന്റെ വര്ഗം 16, പൊതുവ്യത്യാസം 3. ഈ ശ്രേണി എഴുതുക.
f 2 = 16
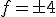
അതായത്,
ആദ്യപദം +4 ഓ -4 ഓ ആകാം. പൊതുവ്യത്യാസം 3. ശ്രേണികള് നിങ്ങള്ക്കെഴുതാമല്ലോ.
എത്ര ശ്രേണികള് കിട്ടി ?
മുമ്പു കണ്ട പരപ്പളവു പ്രശ്നത്തില് എന്തുകൊണ്ട് രണ്ടു പരിഹാരങ്ങള് പരിഗണിച്ചില്ല ?
| Back to Index | അടുത്ത പേജിലേക്ക് |