ഉള്ളടക്കം

തുടര്‍മൂല്യനിര്‍ണ്ണയത്തിന്റെ ഭാഗമായി പൂര്‍ത്തിയാക്കുന്ന ഒരു പ്രവര്‍ത്തനമാണ് പ്രാക്ടിക്കല്‍. രണ്ടാം കൃതി സമവാക്യത്തിന്റെ പരിഹാരം കണ്ടെത്തുന്നതിനുള്ള ഒരു പ്രാക്ടിക്കലാണ് ഇവിടെ കൊടുത്തിരിക്കുന്നത് . x² - 8x - 20 =0 എന്ന രണ്ടാംകൃതി സമവാക്യത്തിന്റെ പരിഹാരം കണ്ടെത്തുന്നത് ഇവിടെ വിവരിക്കുന്നു.

    ഒരു പ്രാക്ടിക്കല്‍ ചെയ്യുമ്പോള്‍ അതിനായി ഉപയോഗിക്കുന്ന സാമഗ്രികളെക്കുറിച്ച് സൂചിപ്പിക്കണം . ഇന്‍സ്റ്റുമെന്റ് ബോക്സ് , ചരടുകള്‍ , പിന്നുകള്‍ ,ഡ്രോയിങ്ങ് ഷീറ്റുകള്‍ ഗ്രാഫ് ഷീറ്റ് ,പശ മുതലായവ ഇതിനവശ്യമാണ്.

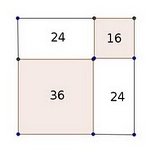
    വലിയ ഗ്രാഫ് ഷീറ്റില്‍ സാമാന്യം വലുപ്പമുള്ള ഒരു സമചതുരം വരക്കുക,അതിന്റെ വശം x ആയി കണക്കാക്കുക. അതിന്റെ രണ്ട് സമീപവശങ്ങള്‍ ചേര്‍ത്ത് മറ്റൊരു സമചതുരം പൂര്‍ത്തിയാക്കുക.അതിന്റെ വശം x-4 ആയിരിക്കണം. അപ്പോള്‍ ഒരു ചോദ്യം ഉയരും . എവിടെ നിന്നാണ് ഈ x-4 വന്നതെന്ന്. x² - 8x - 20 =0 എന്നതിനെ (x-4)² =36 എന്ന് എഴുതാം?
    ആദ്യസമചതുരത്തിനുള്ളില്‍ വരച്ച (x-4)² പരപ്പളവുള്ള സമചതുരത്തിന്റെ രണ്ടു വശങ്ങള്‍ നീട്ടി ആദ്യ സമചതുരത്തിന്റെ മറ്റുരണ്ടു വശങ്ങളെ തൊട്ടാല്‍ ആദ്യ ചതുരം നാലായി ഭാഗിക്കപ്പെടും. അതിനുള്ളില്‍ അവയുടെ പരപ്പളവ് എഴുതാമല്ലോ. ജിയോജിബ്രയില്‍ വരച്ച ചിത്രം കാണുക.
    ഇനി ചെയ്യേണ്ടത് മറ്റൊരു രസകരമായ കാര്യമാണ്. മുകളില്‍ കാണുന്ന ചിത്രത്തില്‍ (x-4)² പരപ്പളവുള്ള ഒരു സമചതുരമുണ്ടല്ലോ? ഇതിന്റെ യഥാര്‍ഥ പരപ്പ് 36 ആണല്ലോ (വര്‍ഗ്ഗത്തികവ് നോക്കുക). മറ്റൊരു ചെറിയ സമചതുരമുണ്ടല്ലോ
ചിത്രത്തില്‍ . അതിന്റെ പരപ്പ് 16 ആണല്ലോ? ഇനി അതുരണ്ടും മാത്രം വരക്കാം. എന്നിട്ട് അതിന്റെ വശങ്ങള്‍ നീട്ടി മറ്റു രണ്ടു സമചതുരങ്ങള്‍ പൂര്‍ത്തിയാക്കാം
     രണ്ടു ചിത്രങ്ങളിലും കാണുന്ന ചതുരങ്ങളും സമചതുരങ്ങളും സര്‍വ്വസമങ്ങളാണ് . ഒരേ പരപ്പളവാണ്. അതിനാല്‍ അതിനാല്‍ 4x-16 = 244x−16=24എന്ന് എഴുതുന്നതില്‍ യുക്തിഭംഗമില്ല. ഇതില്‍ നിന്നും x = 10 എന്നെഴുതാം .പിന്നെ ഒരു കാര്യം . നെഗറ്റീവ് സംഖ്യകളായ പരിഹാരം ഇവിടെ പ്രായോഗികമാകില്ലെന്നു തോന്നുന്നു.

Back to Index

അടുത്ത പേജിലേക്ക്

^{തയ്യാറാക്കിയത്: ഐടി @ സ്കൂള്‍, പൊതുവിദ്യാഭ്യാസ വകുപ്പ്‌, കേരള സര്‍ക്കാര്‍}